The formulae used to change geographic coordinates between geodetic datums are known as similarity transformations.
Coordinate systems used in New Zealand
The formulae used for these transformations are formally defined in the LINZ standard LINZS25000 (Standard for New Zealand Geodetic Datum 2000) (https://linz.govt.nz/regulatory/25000) and are summarised in the associated NZGD2000 fact sheet (LINZG25700) (https://linz.govt.nz/regulatory/25700) and LINZG25703 (Fact Sheet - Datum and Projection Transformations) (https://linz.govt.nz/regulatory/25703).
Standard for New Zealand Geodetic Datum 2000 (LINZS25000)
NZGD2000 fact sheet (LINZG25700)
Fact Sheet - Datum and Projection Transformations (LINZG25703)
For most users the most convenient method of transforming data between datums is to use the online coordinate converter.
Similarity transformations are used to convert a point from one ellipsoid/datum to another. A simple 3-parameter transformation can be used if the geodetic datums have the same orientation and scale, or a 7-parameter transformation is required when the conversion also includes rotation and scale change.
Note that there are 2 common conventions used to define similarity transformations, which use different signs to describe the rotation components: Helmert and Bursa-Wolf. The transformations used in New Zealand, and described here, follow the Helmert convention. Always check transformation software to ensure the correct rotation directions are being applied.
As similarity transformation equations require input coordinates to be cartesian (X,Y,Z), the process of completing either a 3-parameter or 7-parameter transformation involves 3 steps, which are explained below.
Step 1: Changing geographic coordinates to cartesian coordinates
The first step is to convert the geographic coordinates, latitude (Φ), longitude (λ), and height (h), into cartesian coordinates (X,Y,Z):

For these equations ν and e2 are determined using the following formula, and h is the height of the computation point (this is often set to ‘zero’ for horizontal datums).
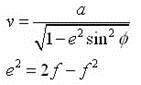
Where, a and f refer to the semi-major axis (a) and the inverse flattening (1/f) of the reference ellipsoid of the geodetic datum.
Step 2: Transformation of cartesian coordinates
The second step is to calculate and apply the transformation.
The 3-parameter transformation, calculates coordinate differences using an X,Y,Z system, defining one datum with its centre at 0,0,0, and the centre of the other datum at a distance (Tx, Ty, TZ) metres away.
The 7-parameter transformation is more complex, as it includes the (Tx, Ty, Tz) shift, as well as three angular rotations around each axis (Rx,Ry,Rz), and a scale factor.
Convergence, scale factors and declination
Step 2a: 3-parameter transformation
The 3-parameter transformation is implemented using the equation:
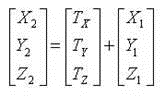
Step 2b: 7-parameter transformation
This is the official formula used to between New Zealand Geodetic Datum 1949 (NZGD1949) and New Zealand Geodetic Datum 2000 (NZGD2000).
New Zealand Geodetic Datum 1949
New Zealand Geodetic Datum 2000
The 7-parameter transformation is a simplified version of the Helmert formulae that applies for small rotation angles.
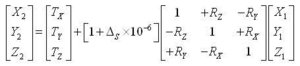
Where the rotation parameters (R) are in radians.
Step 3: Cartesian coordinates to geographic coordinates
The final step is to convert the cartesian coordinates (X, Y, Z) back to into geographic coordinates (latitude (Φ), longitude (λ), and height (h)).
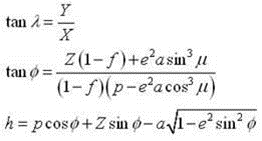
Where a and f refer to the semi-major axis (a) and the inverse flattening (1/f) of the reference ellipsoid
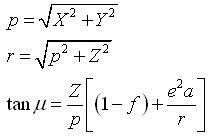
Note: NZGD1949 is a horizontal datum, so for any transformation which includes NZGD1949 the height computed will not be correct.